ECUACIÓN DE LAPLACE EN CILINDRICAS Y ESFERICAS
2o ciclo solucion de la ecuacion de laplace en coordenadas esfericas
العربية. Ecuación diferencial que describe el comportamiento de campos en el espacio libre. El Laplaciano de una función potencial "U" desaparece en un espacio que no contiene fuentes ni sumideros. ( es el operador ''del''.) Los campos gravitatorios, magnéticos, eléctricos y electromagnéticos obedecen la ecuación de Laplace.
Laplaciano en coordenadas cilíndricas YouTube

El sistema de coordenadas cartesianas ofrece una forma sencilla de describir la ubicación de los puntos en el espacio. Sin embargo, algunas superficies pueden ser difíciles de modelar con ecuaciones basadas en el sistema cartesiano.
(PDF) Coordenadas Cartesianas Consideremos la ecuación de Laplace

La ecuación de Laplace es una ecuación diferencial parcial de segundo orden que se puede escribir de la siguiente forma: ∇2ϕ = 0. Aquí, ϕ representa la función potencial y el operador ∇2 es conocido como el operador Laplaciano. En tres dimensiones, el Laplaciano se expresa como: ∇2 = ∂2 ∂x2 + ∂2 ∂y2 + ∂2 ∂z2. La.
122 Electrostática Ecuación de Laplace en cilíndricas simetría en z YouTube

Obtención de la Ecuación de Laplace en coordenadas cilíndricas a partir de la misma en coordenadas rectangulares.
ECUACIÓN DE LAPLACE EN CILINDRICAS Y ESFERICAS

En esta página, resolveremos la ecuación de Laplace en coordenadas esféricas en tres situaciones: La posición de un punto en coordendas esféricas está especificada, por r, los ángulos φ y θ: {x = rsinθcosφ y = rsinθsinφ z = rcosθ. La ecuación de Laplace en coordenadas esféricas es. 1 r2 ∂ ∂ r (r2 ∂ V ∂ r) + 1 r2sinθ ∂.
Clase 06 Ecuación de Laplace en coordenadas cilíndricas, ecuaciones de Bessel YouTube

La ecuación de la conducción del calor en el estado estacionario, independiente del tiempo, es la ecuación de Laplace en coordenadas cilíndricas. 1 ρ ∂ ∂ ρ (ρ ∂ T ∂ ρ) + 1 ρ 2 ∂ 2 T ∂ φ 2 = 0. La solución se escribe como producto de dos funciones una R(ρ) que depende solamente de ρ y otra F(φ), que depende solamente de.
118 Electrostática Ecuación de Laplace en esféricas esfera con campo
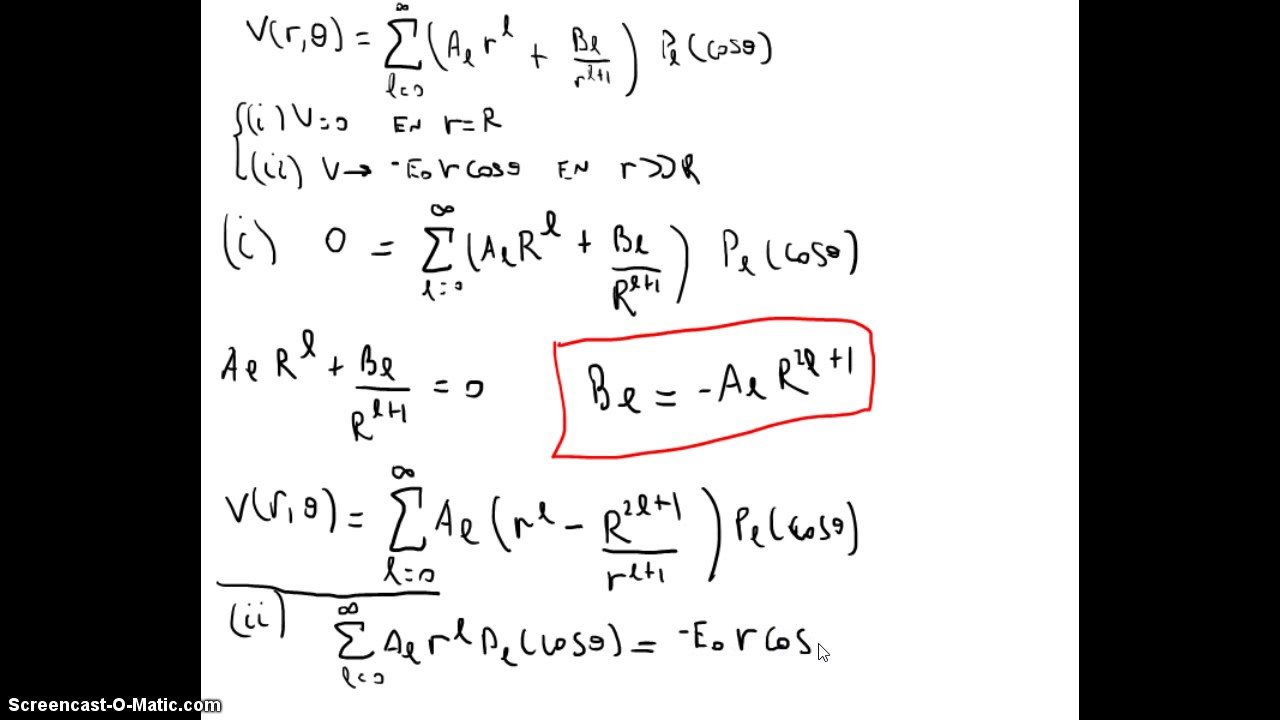
Problema de Dirichlet para un círculo. La ecuación de Laplace se escribe comúnmente simbólicamente como \[\label{eq:2}\nabla ^2u=0,\] donde \(\nabla^2\) se llama el Laplaciano, a veces denotado como \(\Delta\).El Laplaciano se puede escribir en varios sistemas de coordenadas, y la elección de los sistemas de coordenadas suele depender de la geometría de los límites.
Separación de variables. Ecuación de Laplace, caso general, coordenadas cartesianas en 2D. YouTube

Resolvemos la ecuación de Laplace en coordenadas cilíndricas con dos variables. Usamos un ejemplo muy parecido al de la clase 9 en donde un cilindro está inm.
114 Electrostática Ecuación de Laplace en cartesianas caja cubica 3d YouTube

En esta página y en la anterior, resolveremos la ecuación de Laplace en coordenadas cilíndricas para cilindros infintamente largos: Recinto en forma de cuña; Condensador cilíndrico; Dos cilindros concéntricos; Para un recinto cilíndrico infinitamente largo, el potencial no depende de z. La ecuación de Laplace se reduce a
2o ciclo solucion de la ecuacion de laplace en coordenadas esfericas
La Ecuación de Laplace en coordenadas cilíndricas es: (111) con V función de r, q, z. Comenzaremos por obtener la solución general en donde sólo se tiene dependencia radial, para luego tratar el caso en donde no se tiene dependencia en la coordenada Z, y finalmente donde se tiene dependencia en las tres coordenadas. Dependencia Radial.
115 Electrostática Ecuación de Laplace en esféricas simetría azimutal

Cilindro infinitamente largo, independiente de la coordenada z. La posición de un punto en coordendas cilíndricas está especificada, por ρ, el ángulo φ y z: x=ρ ·cos φ, y=ρ ·sin φ, z=z. En coordenadas cilíndricas la ecuación de Laplace se escribe. 1 ρ ∂ ∂ρ (ρ∂V ∂ρ)+ 1 ρ2 ∂2V ∂φ2 + ∂2V ∂z2 =0 1 ρ ∂ ∂ ρ.
Laplaciano en coordenadas cilíndricas Laplaciano en coordenadas Operador Laplace o 2 f de

El problema de Dirichlet para la ecuación de Laplace consiste en hallar una solución en algún dominio tal que sobre su contorno o frontera es igual a una función determinada: { =, =,Como el operador de Laplace aparece en la ecuación del calor, una interpretación física de este problema es lo siguiente: fijar la temperatura sobre el contorno del dominio de acuerdo a una especificación.
Ecuación de transmisión de calor por coordenadas cilíndricas UPV YouTube

El core ciente para el t ermino dominante (menor potencia) j= 2 es cero si = 0 o 1; a 0 = 0 no es una opci on v alida porque por de nici on el primer t ermino en la expansi on tiene un coe ciente que no se anula.
Separación de variables. Ecuación de Laplace en coordenadas polares, solución general. YouTube

lim t → ∞ut(x, y, t) = 0. y la temperatura se aproxima a una distribución de estado estacionario u = u(x, y) que satisface. uxx + uyy = 0. Esta es la ecuación de Laplace. Esta ecuación también surge en aplicaciones a la mecánica de fluidos y a la teoría del potencial; de hecho, también se le llama la ecuación de potencial.
123 Electrostática Ecuación de Laplace en cilíndricas tubo cilíndrico

Ahora consideraremos problemas de valor límite para la ecuación de Laplace sobre regiones con límites mejor descritos en términos de coordenadas polares. En este caso es apropiado considerar u como función (r, θ) y escribir la ecuación de Laplace en forma polar como. urr + 1 rur + 1 r2uθθ = 0, donde. r = √x2 + y2 and θ = cos − 1x.
110 Electrostática Ecuación de Laplace en cartesianas ejemplo dos placas

La solución bidimensional que encontramos está relacionada al análisis complejo. Debido a las condiciones de Cauchy-Riemann que satisface una función analítica f (z), Im(f (z)) y Re(f (z)) satisfacen la ecuación de Laplace. Tema de charla: Métodos de variable compleja para encontrar el potencial en dos dimensiones.
.